
There exist hundreds of versions of the radar range equation. Below is one of the more basic forms for a single antenna system (same antenna for both transmit and receive). The maximum detection is when the target is in the center of the beam.

The variables in the above equation are constant and radar dependent except target RCS. Transmit power will be on the order of 1 mW (0 dBm) and antenna gain around 100 (20 dB) for an effective radiated power (ERP) of 100 mW (20 dBm). Minimum detectable signals are on the order of picowatts; RCS for an automobile might be on the order of 100 square meters. The accuracy of the radar range equation is only as good as the input data.
Minimum detectable signal (Pmin) depends on receiver bandwidth (B), noise figure (F), temperature (T), and required signal-to-noise ratio (S/N). A narrow bandwidth receiver will be more sensitive than a wider bandwidth receiver. Noise figure is a measure of how much noise a device (the receiver) contributes to a signal: the smaller the noise figure, the less noise the device contributes. Increasing temperature affects receiver sensitivity by increasing input noise.
| Pmin = k T B F (S/N)min |
Pmin = Minimum Detectable Signal
k = Blotzmann's Constant = 1.38 x 10-23 (Watt*sec/°Kelvin)
T = Temperature (°Kelvin)
B = Receiver Bandwidth (Hz)
F = Noise Factor (ratio), Noise Figure (dB)
(S/N)min = Minimum Signal to Noise Ratio
The available input thermal noise power (background noise) is proportional to the product kTB where k is Boltzmann's constant, T is temperature (degrees Kelvin) and B is receiver noise bandwidth (approximately receiver bandwidth) in hertz.
| kTB = -174 dBm/Hz |
The radar range equation above can be written for power received as a function of range for a given transmit power, wavelength, antenna gain, and RCS.
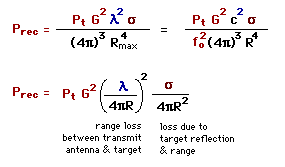
|
Prec = Power Received Pt = Transmit Power fo = Transmit Frequency Lamda = Transmit Wavelength |
G = Antenna Gain Sigma = Radar Cross Section R = Range c = Speed of Light |
Radar has a range loss inversely proportional to range to the 4th power (1/R4). Radio communications range losses are inversely proportional to range squared (one-way path is 1/R2). Signal power received (by a radar detector), where Gdet is detector antenna gain, can be expressed as shown below. By substituting radar detector minimum signal for power received, detector maximum range can be estimated if radar power and antenna gain are known (ERP -- effective radiated power).
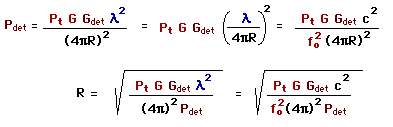
|
Pdet = Power Received by Detector Gdet = Detector Antenna Gain |
Radar propagation loss is proportional to 1/R4 (2-way signal path), while a radar detector would be picking up the signal on the direct (1-way) path with loss proportional to 1/R2 (a hugh advantage for the detector). Another hugh advantage is the radar is receiving a reflection (RCS), most of the reflective energy is directed away from the radar. The radar has the advantage of a much larger antenna (more gain) and more sensitive (to radar signal) receiver. However, good radar detector should be able to detect a radar before the radar detects the vehicle, but not always.